Program Updates: Science and Math – April 2025
SCIENCE
Grade 6 (Kristin)
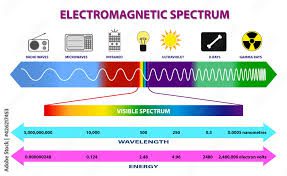
Why do radios and cell phones lose reception when you go through a tunnel? How does a remote control turn on a TV? These, and other questions related to the electromagnetic spectrum, are top of mind in 6th grade science right now. What do all these different size waves do, and how do we use them in our everyday lives? Astronomers use the different waves of the Electromagnetic Spectrum to study objects millions of light years away.
If you haven’t had a chance to check out the images from the James Webb telescope, here is a link showing these phenomenal views deep into space!
Grade 7 (Virgil)
Seventh graders are starting a unit on genetics. They began by observing photos of two cattle, one of whom has significantly more muscle than the other. After developing initial models for the possible causes of these differences in musculature, students used videos, photos, data sets, and readings to investigate what causes an animal to get extra-big muscles. Students figure out how muscles typically develop as a result of environmental factors such as exercise and diet. Then, students worked with cattle pedigrees, including data about chromosomes and proteins, to figure out genetic factors that influence the heavily muscled phenotype and explore selective breeding in cattle.
Later they will use what they’ve learned from explaining cattle musculature to help them explain other trait variations they’ve seen. They will investigate plant reproduction, including selective breeding and asexual reproduction (in plants and other organisms) and other examples of traits that are influenced by genetic and environmental factors. Students will figure out that environmental and genetic factors together play a role in the differences we see among living things.

Grade 8 (Kristin)
Water was successfully desalinated, and we’ve moved on to studying weather and answering the question, “Why does a lot of hail, rain and snow fall at some times but not others?” Students looked at images of hailstones and, to learn more about how hail forms, listened to a fascinating story about a man who ejected from an airplane and was tossed up and down inside a hailstorm for 45 minutes before landing… in a tree, We also learned about the adage, “Dew on the grass, no rain will come to pass.”



MATH
Grade 6 (Scott)
Sixth grade mathematicians are just wrapping up our exploration/preview of variable expressions and algebraic equations. While getting to know coefficients and variables, students also have dived into exponents, (particularly squared and cubed numbers within the context of a cube’s surface area and volume), the Distributive Property, Independent and Dependent variables, and Equivalency. We represented equations with Balance Diagrams and Tape Diagrams, and ultimately compared solution sets in tables, graphs, and equations.
I think it’s fair to say the topic we are really looking forward to is… Spring Break, but we had to admit this diagram of exponents in action was pretty cool.

Grade 7 (Virgil)
In our current unit, the 7th graders are deepening their algebraic reasoning as they write and solve equations of the forms px+q=r and p(x+q)=r and inequalities of the forms of pxr and p(x+q)r.
Students will build on this work in future units when they solve equations that have a variable on both sides of the equal sign, and when they work with systems of equations.
Grade 8 (Scott)
At last, quadratics…
Last week, we connected the standard form of a linear equation to the launching of a T-shirt in a gravity-less environment. Then, thanks to Galileo and some keen observation, we were able to build in gravity to make it a quadratic (-16x^2 + 90x + 5) and graph the t-shirt’s distance from the ground as a parabola.
We still have some sense-making to do to relate equations to their graphs and to find some other forms for quadratics that will allow us to find zeroes (x-intercepts) and vertices (max. or min.) and build equations effectively from a variety of situation descriptions and data.
It’s a definite step up from our last unit with exponential functions, and with some good spring concentration, we’ve got this!
